delay-discounting-analysis

Discount functions available

A number of discounting models are available, all with the following basic form. The models differ in either a) presence/absence of hyperpriors, b) the discount functions in the data generating process which specifies the response probability.

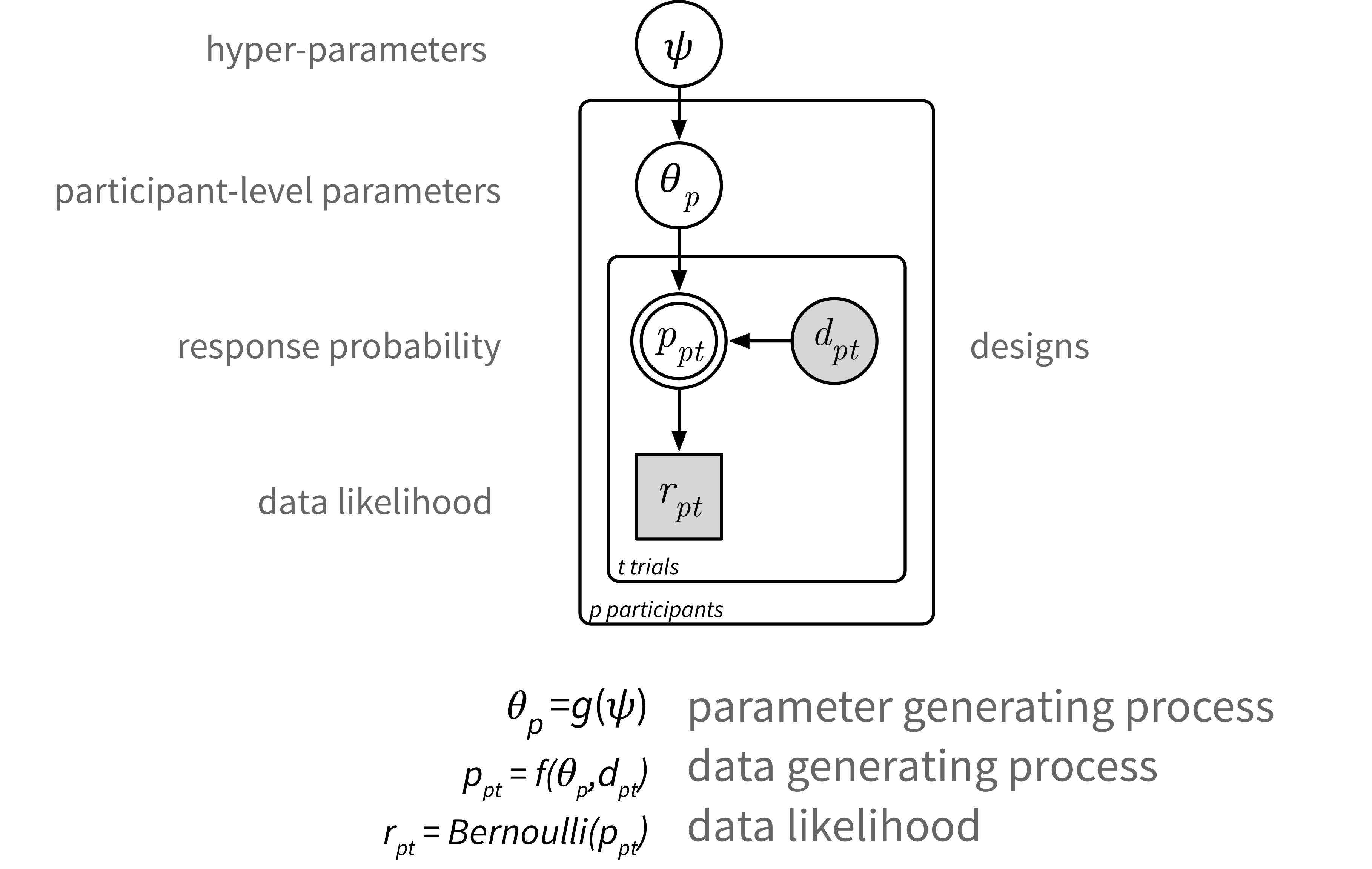
The ‘data generating process’ describes the response probability. This consists of the psychometric link function which captures response errors, and the discount function which computes the present subjective value of prospects. See the paper for details.

Discount function	Equation	Model suffix	Main parameters
Exponential	exp(-k*D)	*Exp1	k
Hyperbolic	1/(1+k*D)	*LogK	logk
Hyperbolic (with magnitude effect)	1/(1+[exp(m*log(R)+c)]*D)	*ME	m, c
Hyperboloid	1/[(1+k*D)^S]	*Hyperboloid	logk, S
Beta Delta	beta*delta^D	*BetaDelta	beta, delta

In the equations, D = delay, and R = reward.

Detailed information on discount functions

Note that Separate, Mixed and Hierarchical refers to the level of parameter pooling (hierarchical inference). See the page Decide on level of parameter pooling for more information on this.

Exponential discounting

Model name	Fixed Effects	Random Effects (by-participant)	Hyper-priors (thus shrinkage to group mean)
ModelSeparateExp1	-	k, alpha, epsilon	-
ModelMixedExp1	-	k, alpha, epsilon	alpha, epsilon
ModelHierarchicalExp1	-	k, alpha, epsilon	k, alpha, epsilon

Hyperbolic discounting

Model name	Fixed Effects	Random Effects (by-participant)	Hyper-priors (thus shrinkage to group mean)
ModelSeparateLogK	-	logk, alpha, epsilon	-
ModelMixedLogK	-	logk, alpha, epsilon	alpha, epsilon
ModelHierarchicalLogK	-	logk, alpha, epsilon	logk, alpha, epsilon

Hyperbolic discounting, with magnitude effect

Model name	Fixed Effects	Random Effects (by-participant)	Hyper-priors (thus shrinkage to group mean)
ModelSeparateME	-	m, c, alpha, epsilon	-
ModelMixedME	-	m, c, alpha, epsilon	alpha, epsilon
ModelHierarchicalME	-	m, c, alpha, epsilon	m, c, alpha, epsilon (model focussed upon in the paper)

Prior over slope of the magnitude effect

The prior over m was well thought out and is described in depth in the Appendix of the paper. So there should be little need to change this, aside from perhaps if you were investigating a specific sub-population of people who deviated from the general population in some way. Of course, as we get more information about the magnitude effect, the prior over m could be updated to reflect this increased knowledge.

Prior over the intercept of the magnitude effect

The prior over c was kept very uninformative, on the basis that it reflects a scaling up or down of discount rates. This can vary a lot between participants, and of course the intercept will change depending upon the unit of reward, is it £, €, or $, or even in number of chocolates? Therefore people may well want to provide a bit more of an informative prior over the intercepts which is appropriate for your research context.

Hyperboloid

Hyperboloid discounting, of the form 1/[(1+kD)^S]. This is equivalent to exponential discounting of subjective time (according to Webber’s Law).

Model name	Fixed Effects	Random Effects (by-participant)	Hyper-priors (thus shrinkage to group mean)
ModelSeparateHyperboloid	-	logk, S, alpha, epsilon	-
ModelMixedHyperboloid	-	logk , S, alpha, epsilon	alpha, epsilon
ModelHierarchicalHyperboloid	-	logk , S, alpha, epsilon	logk , S, alpha, epsilon

Beta-Delta

The discount factor is beta*delta^D, see (Laibson, 1997).

I highly recommend updating the priors for this discount function.

Model name	Fixed Effects	Random Effects (by-participant)	Hyper-priors (thus shrinkage to group mean)
ModelSeparateBetaDelta	-	beta, delta, alpha, epsilon	-
ModelMixedBetaDelta	-	beta , delta, alpha, epsilon	alpha, epsilon
ModelHierarchicalBetaDelta	-	beta , delta, alpha, epsilon	beta, delta, alpha, epsilon