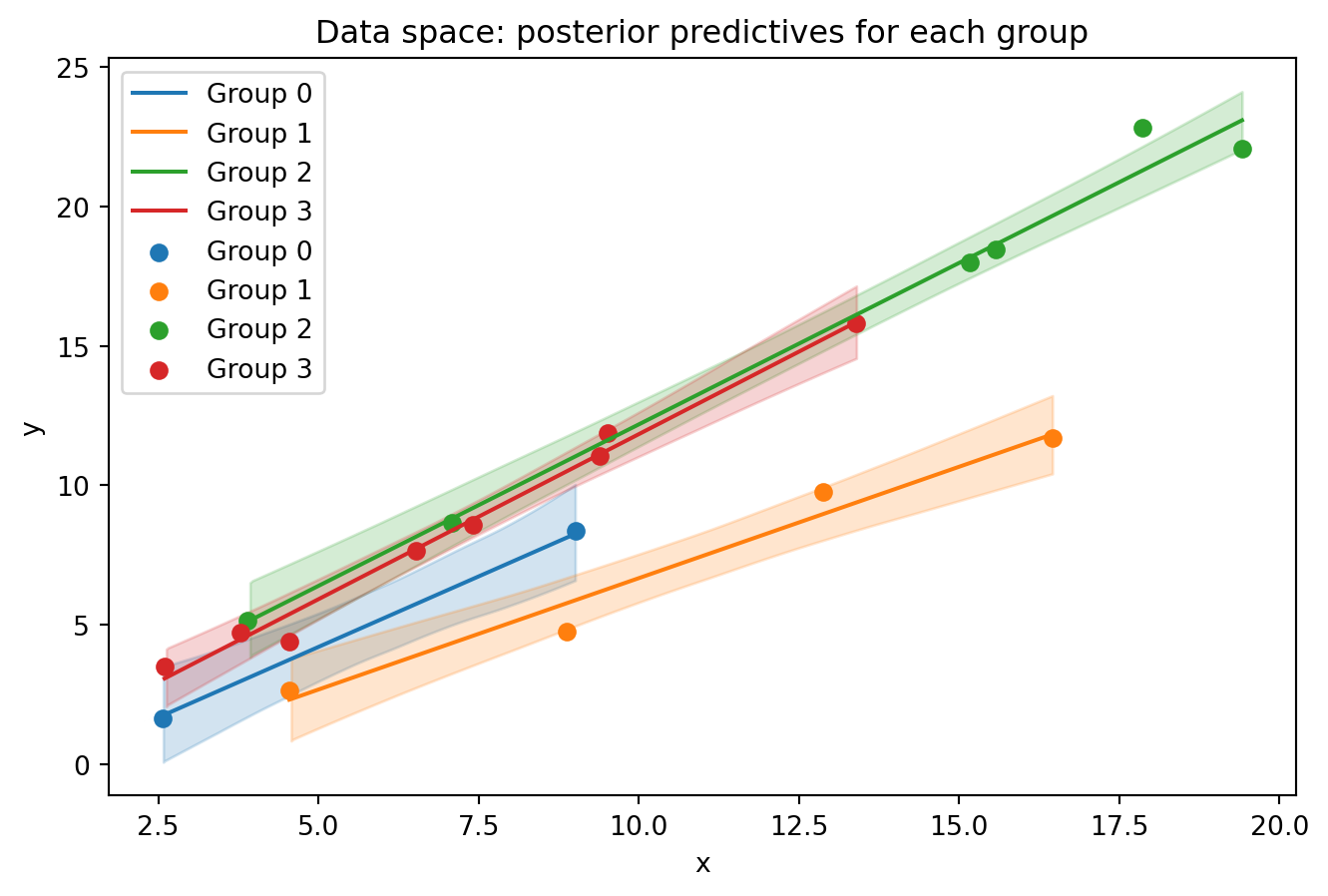
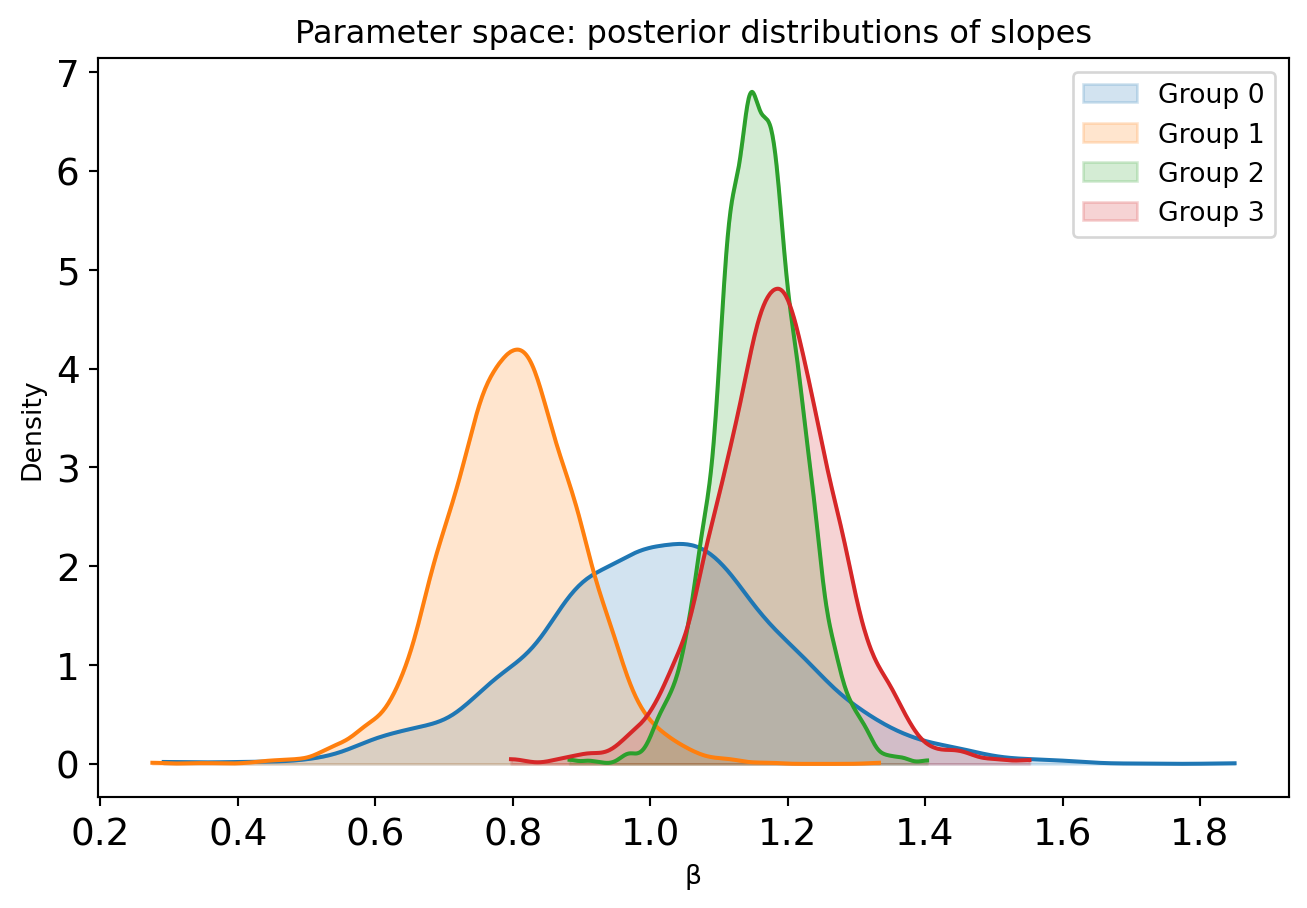
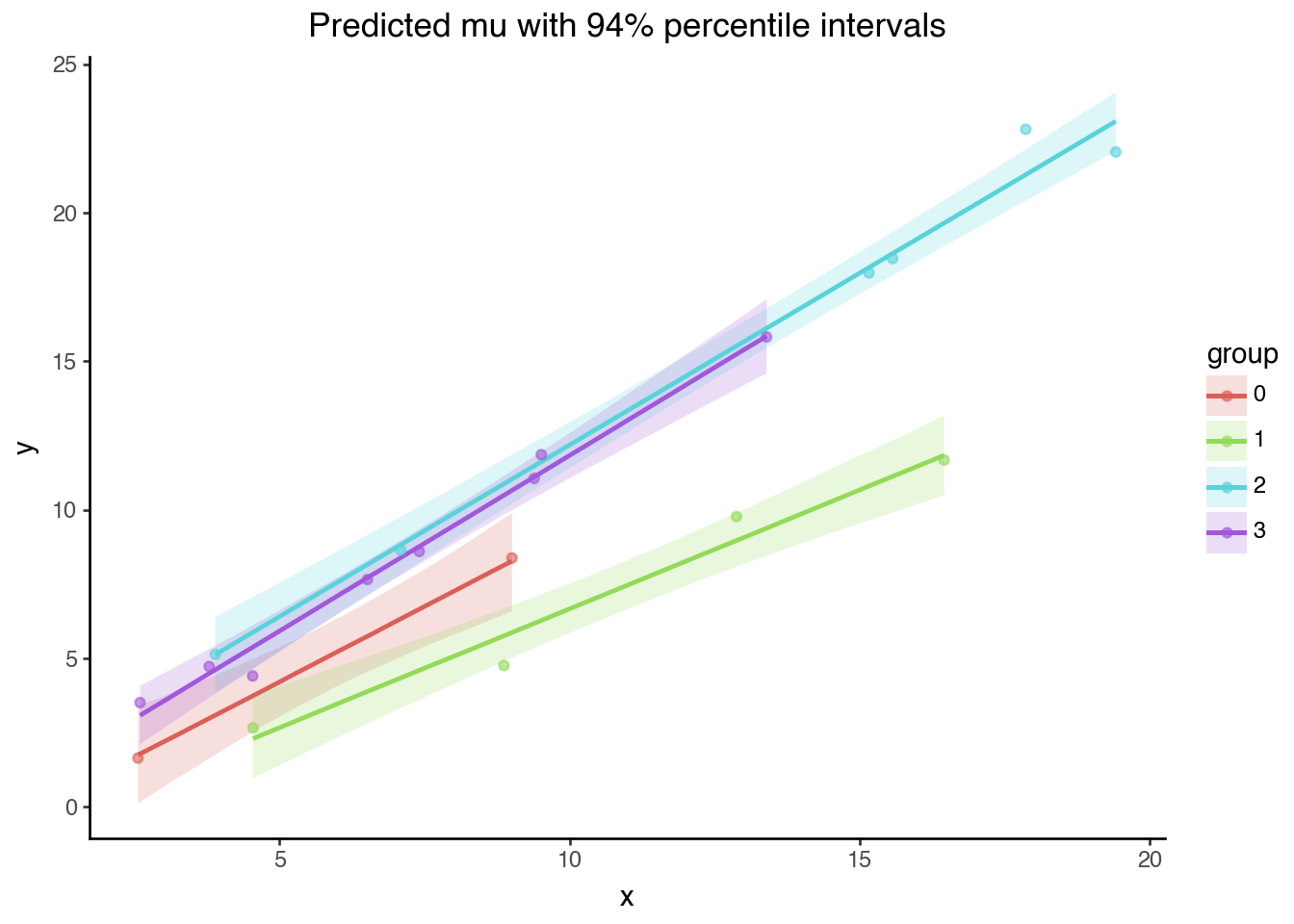
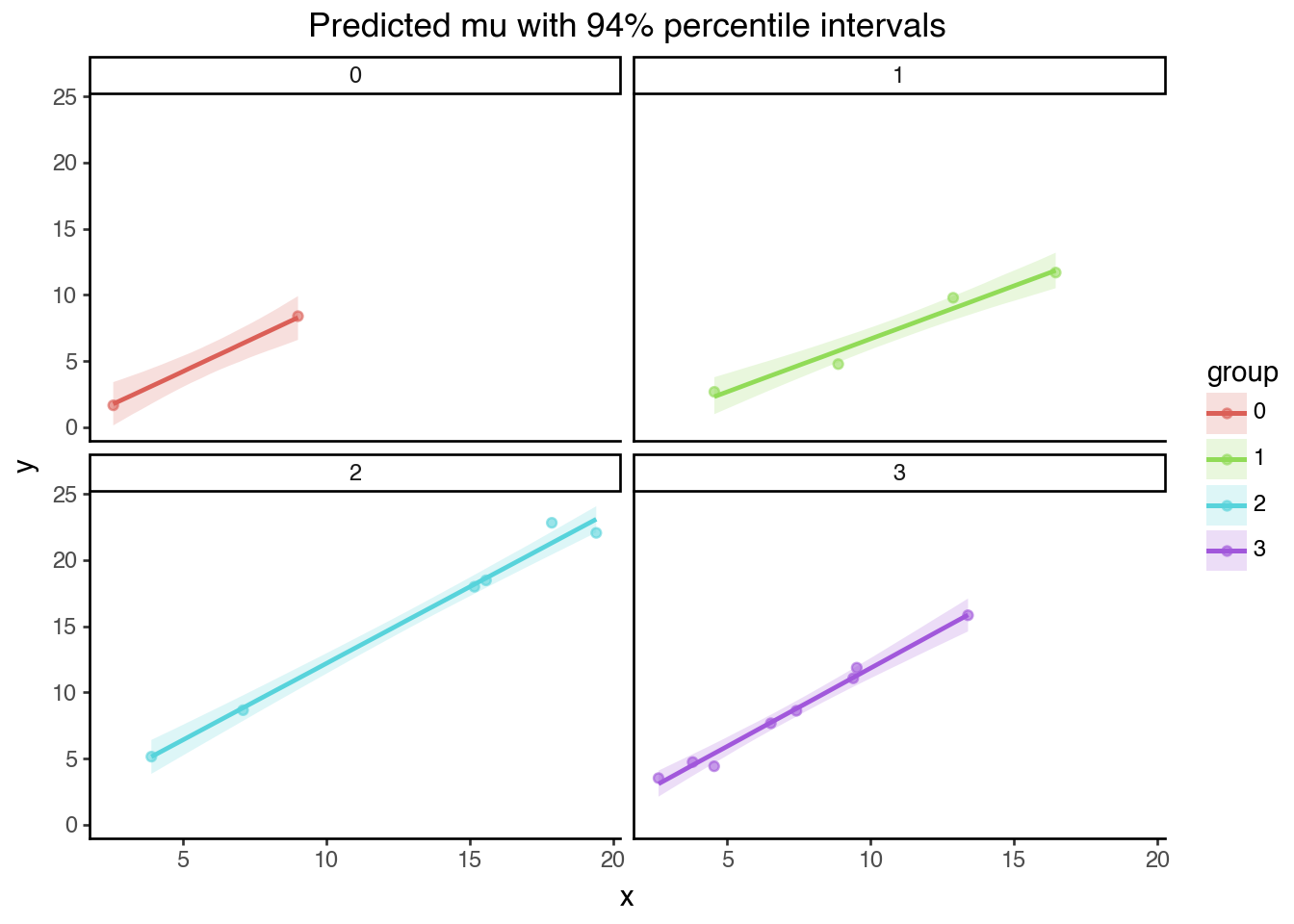
Code
import arviz as az
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import pymc as pm
import seaborn as sns
from plotnine import (
ggplot,
aes,
stat_summary,
facet_wrap,
theme_classic,
labs,
geom_density,
geom_point,
)
plt.rcParams["figure.figsize"] = [8, 5]
%config InlineBackend.figure_format = 'retina'
RANDOM_SEED = 42
rng = np.random.default_rng(RANDOM_SEED)
# generate data ------------------------------------------------------------------------
n_groups = 4
group_size = [2, 4, 6, 8]
# Group-specific parameters
slopes = rng.normal(1, 0.2, size=n_groups)
intercepts = rng.normal(0, 1, size=n_groups)
# Generate data
data = []
for i in range(n_groups):
n = group_size[i]
x_vals = np.sort(rng.uniform(0, 20, size=n))
noise = rng.normal(0, 1, size=n)
y_vals = slopes[i] * x_vals + intercepts[i] + noise
group_labels = np.full(n, i)
data.append(pd.DataFrame({"x": x_vals, "y": y_vals, "group": group_labels}))
# Combine all groups into a single DataFrame
df = pd.concat(data, ignore_index=True)
df["group"] = df["group"].astype("category")
# Build a PyMC model -------------------------------------------------------------------
prior_mean = 0
prior_std = 1
x_data = df.x.values
y_data = df.y.values
coords = {"groups": df["group"].cat.categories, "obs_ind": df.index}
with pm.Model(coords=coords) as _m:
x = pm.Data("x", x_data, dims="obs_ind")
y = pm.Data("y", y_data, dims="obs_ind")
group = pm.Data("group", df["group"].cat.codes.values, dims="obs_ind")
# priors
intercept = pm.Normal("intercept", mu=0, sigma=10, dims=["groups"])
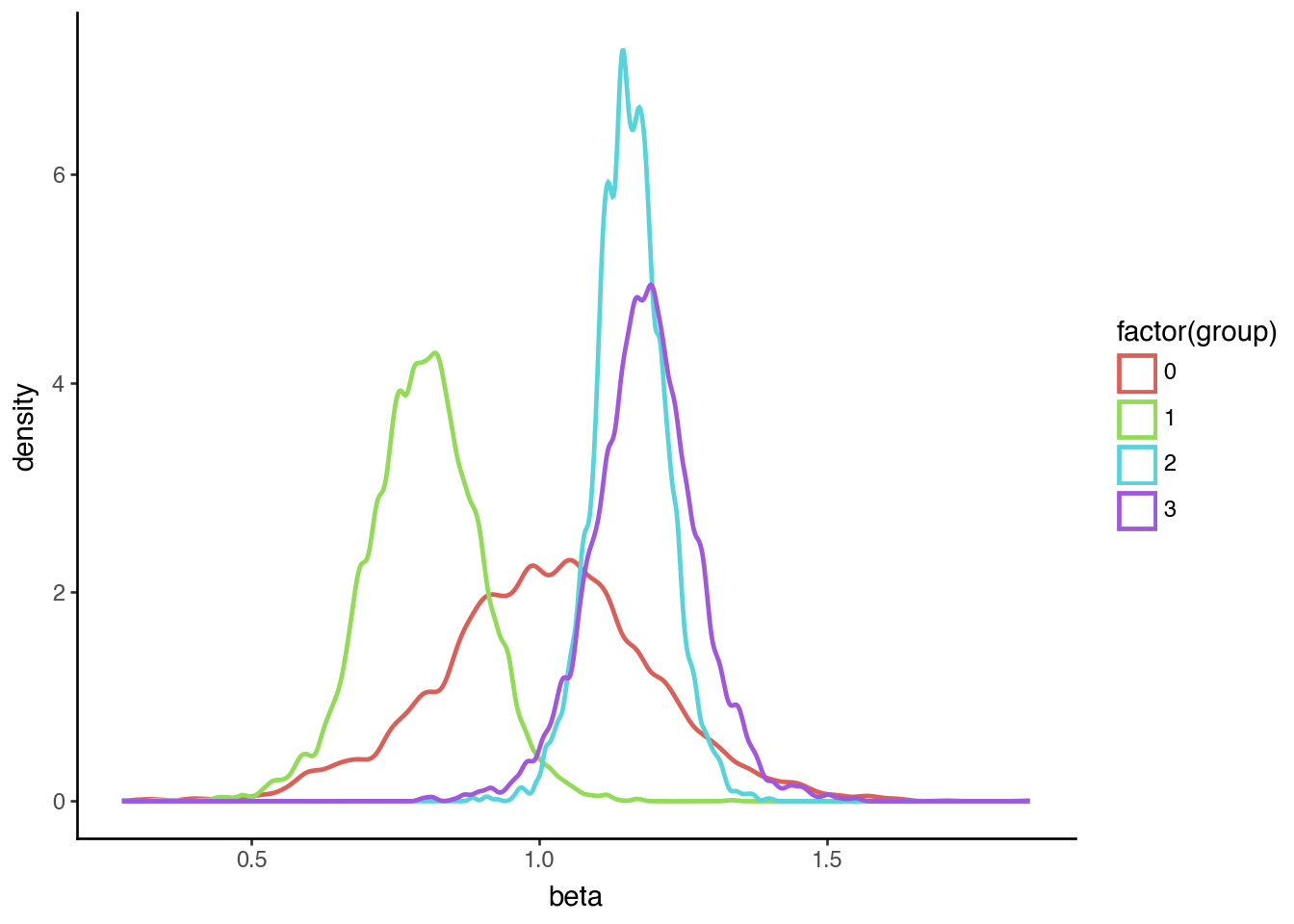
beta = pm.Normal("beta", mu=prior_mean, sigma=prior_std, dims=["groups"])
sigma = pm.HalfNormal("sigma", sigma=5)
# likelihood
mu = pm.Deterministic("mu", intercept[group] + beta[group] * x, dims="obs_ind")
pm.Normal("obs", mu=mu, sigma=sigma, observed=y, dims="obs_ind")
# sample
idata = pm.sample()
# Generate a grid of points to evaluate on ---------------------------------------------
n_interp_points = 20
xi = np.concatenate(
[
np.linspace(group[1].x.min(), group[1].x.max(), n_interp_points)
for group in df.groupby("group")
]
)
g = np.concatenate([[i] * n_interp_points for i in range(n_groups)]).astype(int)
predict_at = {"x": xi, "group": g, "y": np.zeros_like(xi)}
# Posterior prediction on the grid of points -------------------------------------------
coords = {"groups": predict_at["group"], "obs_ind": np.arange(len(xi))}
with _m:
pm.set_data(predict_at, coords=coords)
idata.extend(
pm.sample_posterior_predictive(
idata,
var_names=["mu", "y"],
random_seed=rng,
progressbar=False,
predictions=True,
)
)